At every turn in a non-technical post about AI for broader audience an author deems their duty to mention a deep learning as panacea for all woes. Well, it’s not. Deep learning is just one of various models, which might or might not perform better then the other techniques. At the end of the day, in a nutshell, it’s just regular neural networks with multiple hidden layers between the input and output layers (well, it’s rather a oversimplification, but you got it right). In this post I am curious whether it’s possible for neural networks approach to beat our best model so far (GAM with response’s inverse Gaussian distribution).

Disclaimer: This post is outdated and was archived for back compatibility: please use with care! This post does not reflect the author’s current point of view and might deviate from the current best practices.

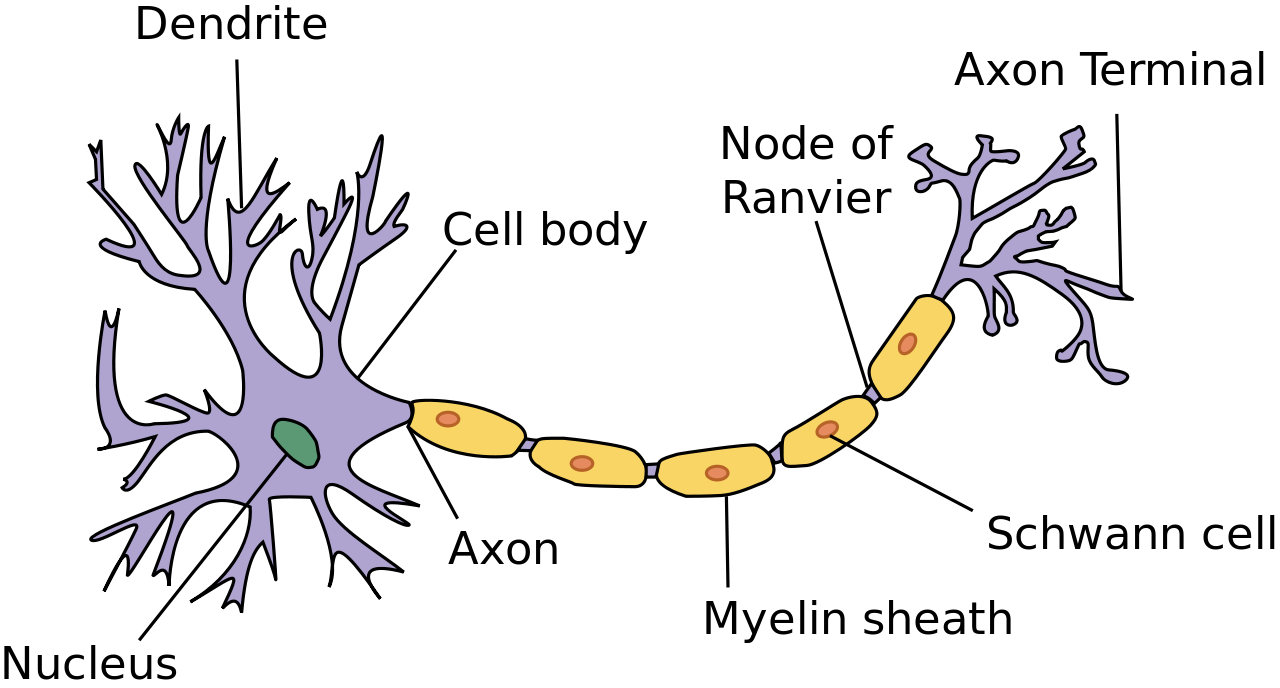
The nice thing about neural networks is it allows for interactions between variables. Remember we included several interaction terms to our simple linear, GLM and GAM models? The construction of neural networks’ model assumes much more complicated interactions, we do not have to worry about that. The more hidden layers we use the more complex these interactions can be.

When at first I tried to use TensorFlow and keras I admit my guilt to R users, I did it in Python. Let me just quickly go over the code chunks and I will come back to R (the code of which is pretty similar).

First, libraries and data should be loaded. As API to TensorFlow the package keras is used, and further, I load pandas to enable DataFrame, as well as numpy’s arrays. Also the regressors (area, rooms) and outcomes (price) are stored in separate variables.

import keras
from keras.layers import Dense
from keras.models import Sequential

import pandas as pd
import numpy as np

property = pd.read_csv('/Users/irudnyts/Documents/data/dortmund.csv')
x = property[["area", "rooms"]].values
y = property[["price"]].values

We need to initialize Sequential model (layers are connected sequentially). We use a neural network with two hidden layers, each of 50 neurons, and a rectified linear unit (ReLU) activation function. Input layer has 2 neurons (area and rooms), and for output layer we have only one output neuron (price). We use standard adam (Adaptive Monument Estimation) optimizer and standard mean squared error for loss (objective) function. Finally we slightly increase number of epochs to 15 for a fit.

model = Sequential()

model.add(Dense(50, activation = 'relu', input_shape = (2,)))
model.add(Dense(50, activation = 'relu'))
model.add(Dense(1))

model.compile(optimizer = 'adam', loss = 'mean_squared_error')
model.fit(x = x, y = y, validation_split = 0.3, epochs = 15)

After the model is specified, compiled, and fitted we can predict and calculate in-sample RMSE.

predicted = model.predict(x = x)

np.sqrt(np.mean((predicted - y) ** 2))
# 166.2982065207604

For in-sample RMSE the result is not bad. However, it was only a first quick and dirty try. At this moment I decided to switch back to R, and here the equivalent code:

packages <- c("ggplot2", "magrittr", "keras", "vtreat")
sapply(packages, library, character.only = TRUE, logical.return = TRUE)

property <- read.csv("/Users/irudnyts/Documents/data/dortmund.csv")
x <- property[, 2:3] %>% as.matrix()
y <- property[, 1]

model <- keras_model_sequential()

model %>%
    layer_dense(units = 50, activation = "relu", input_shape = 2) %>%
    layer_dense(units = 50, activation = "relu") %>%
    layer_dense(units = 1)

model %>% compile(
    loss = "mean_squared_error",
    optimizer = optimizer_adam()
)

model %>% fit(x = x, y = y, epochs = 15)

pred <- model %>% predict(x = x)

sqrt(mean((pred - y) ^ 2))
# 166.152

Looks pretty similar to Python code, right? OK, let’s play around with tuning parameters and empirically find the optimal ones. For this purpose, we define a function that calculates RMSE for neural network with a given number of layers and neurons (assuming each layer has the same number of neurons). Note, while fitting a model we use custom stopping time, i.e. if the mean squared error is not improved more than min_delta = 0.01, then train is stop at current epoch.

get_rmse <- function(n_layers, n_neurons) {
    stopifnot(n_layers < 2)
    model <- keras_model_sequential()
    model %>%
        layer_dense(units = n_neurons, activation = "relu", input_shape = 2)
    for(i in 2:n_layers) {
        model %>%
            layer_dense(units = n_neurons, activation = "relu")
    }
    model %>% layer_dense(units = 1)

    model %>% compile(
        loss = "mean_squared_error",
        optimizer = optimizer_adam()
    )

    model %>% fit(x = x, y = y, epochs = 15,
                  callbacks = callback_early_stopping(min_delta = 0.01,
                                                      monitor = 'loss'))

    pred <- model %>% predict(x = x)
    sqrt(mean((pred - y) ^ 2))
}

Then, we train models with 50 neurons and several levels of layers, namely from 2 to 5:

layers_summary <- data.frame(n_layers = 2:5,
                             rmse = sapply(2:5, get_rmse, n_neurons = 50))
# n_layers     rmse
#        2 166.7639
#        3 165.5580
#        4 165.2328
#        5 164.3651

It seems that 2 layers is more than enough. Let’s now define the number of neurons for each layer:

neurons <- c(seq(from = 10, to = 20, by = 2), seq(from = 30, to = 100, by = 10))
neurons_summary <- data.frame(n_neurons = neurons,
                              rmse = sapply(neurons, get_rmse, n_layers = 2))
# n_neurons     rmse
#        10 296.4352
#        12 165.5779
#        14 167.7926
#        16 210.7701
#        18 166.0520
#        20 166.3228
#        30 165.0766
#        40 165.8220
#        50 165.6295
#        60 165.6339
#        70 165.5375
#        80 165.9305
#        90 164.7960
#       100 164.7582

The model with around 20 neurons looks stable. Thus, for our final model we use 2 layers with 20 neurons to calculate our-of-sample RMSE. The model will use slightly larger number of potential epochs, since we decrease min_delta to 0.0005 to let the model train a bit more.

set.seed(3)
folds <- kWayCrossValidation(nRows = nrow(property), nSplits = 3)

pred <- rep(NA, nrow(property))
for(fold in folds) {
    model <- keras_model_sequential()
    model %>%
        layer_dense(units = 20, activation = "relu", input_shape = 2) %>%
        layer_dense(units = 20, activation = "relu") %>%
        layer_dense(units = 1)
    model %>% compile(
        loss = "mean_squared_error",
        optimizer = optimizer_adam()
    )
    model %>% fit(x = x[fold$train, ], y = y[fold$train],
                  epochs = 30,
                  callbacks = callback_early_stopping(monitor = "loss",
                                                      min_delta = 0.0005))

    pred[fold$app] <- model %>% predict(x = x[fold$app, ])
    rm(model)
}

sqrt(mean((pred - y) ^ 2))
# 165.5461

Fortunately or unfortunately, the model has not outperform our previous models, and the leader is still GAM with IG outcome. On the other hand, we have used the simplest (and when I am saying simplest I do mean simplest) neural networks. With this post I finish the cycle of Dortmund real estate data analysis.