In pervious posts traditional regression models were fitted to real estate data. In this post tree-based models, namely random forests and gradient boosting, are trained to predict prices of the rent. These methods typically outperform traditional regression models yielding smaller errors. Furthermore, tree-based methods are much more robust to overfitting, which makes them superior in terms of prediction. However, the main disadvantage (and the reason why there is no love in insurance industry) is difficulties with interpretability.

Disclaimer: This post is outdated and was archived for back compatibility: please use with care! This post does not reflect the author’s current point of view and might deviate from the current best practices.

Random forests

Originally random forests are implemented in randomForest package. There is also a faster implementation in ranger package, which is used further. As usual, we start with some preliminary code to clean out the memory, load packages and data.

packages <- c("ggplot2", "magrittr", "vtreat", "ranger", "xgboost", "caret")
sapply(packages, library, character.only = TRUE, logical.return = TRUE)

theme_set(theme_bw())
theme_update(text = element_text(size = 24))

rm(list = ls())

setwd("/Users/irudnyts/Documents/data/")
property <- read.csv("dortmund.csv")
set.seed(1)

For random forests there is a hyperparameter mtry determining the number of columns to split in each node. As long as we have only two columns, we set mtry = 2 (the model with default mtry = 1 yields higher RMSE). We also use default number of trees (500 trees). The main function to run the regression is ranger. The function predict(.ranger) behaves a bit differently from other methods. Instead of returning a vector, it returns a list of vectors of class ranger.prediction. Thus, we need to extract predictions form that class.

rf <- ranger(formula = price ~ area + rooms, data = property, mtry = 2)
predicted <- predict(rf, property)
(predicted$predictions - property$price) ^ 2 %>% mean() %>% sqrt()
# [1] 93.07542

Random forests model outperform all traditional regression models in previous posts in terms of in-sample RMSE. Let’s now cross-validate model by looking at out-of-sample RMSE:

property$pred_rf <- NULL

folds <- kWayCrossValidation(nRows = nrow(property), nSplits = 3)

for(fold in folds) {
    rf <- ranger(formula = price ~ area + rooms,
                 data = property[fold$train, ],
                 mtry = 2)
    property[fold$app, "pred_rf"] <-
        predict(rf, property[fold$app, ])$predictions
}

(property$price - property$pred_rf) ^ 2 %>% mean() %>% sqrt()
# [1] 152.3637

The out-of-sample RMSE is comparable with one returned by linear model, but larger than for GAM IG.

Gradient boosting

This methods iteratively optimize the RMSE (or other accuracy measure) on training data. Thus, gradient boosting is more exposed to overfit. In order to get the optimal ‘nrounds’ (the maximum number of iterations) we need to use cross-validation technique, implemented in xgb.cv, which also calculates out-of-sample RMSE. The number of folds we keep equals to $3$, to be consistent with pervious analysis. The learning rate parameter is set to be $0.1$, a little bit less than default ($0.3$), implying robustness to overfit, but also slower speed.

xg <- xgb.cv(data = as.matrix(property[, 2:3]),
             label = property[, 1],
             nfold = 3,
             nrounds = 500,
             metrics = "rmse",
             eta = 0.1)
which.min(xg$evaluation_log$test_rmse_mean)
# [1] 32
ggplot(data = xg$evaluation_log) + geom_line(aes(x = iter, y = test_rmse_mean))

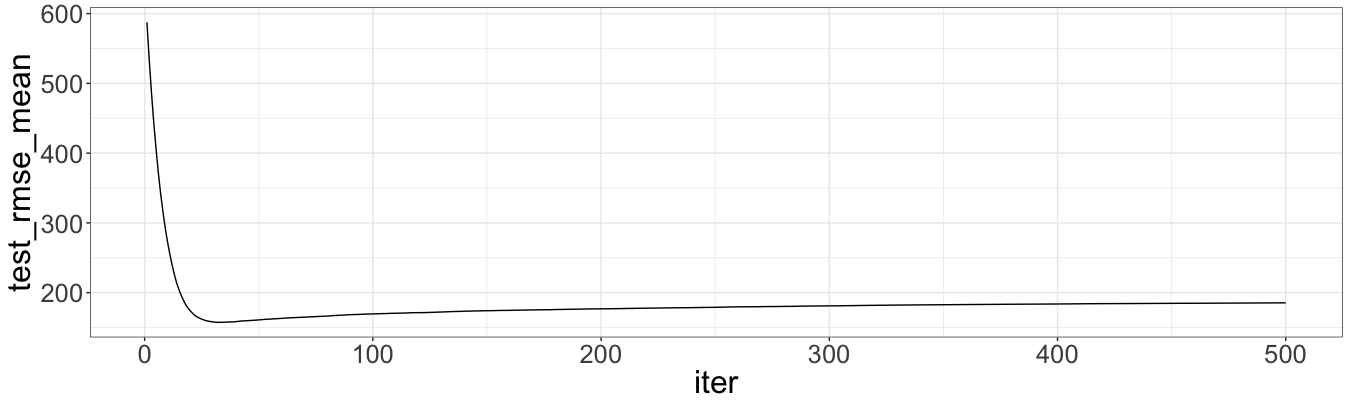
The minimum out-of-sample RMSE is showed by the model with nrounds = 32. This value is approximate and depends on a seed. We use nrounds = 40. Let’s calculate RMSE for the optimal model and then out-of sample RMSE:

xg <- xgboost(data = as.matrix(property[, 2:3]),
              label = property[, 1],
              nfold = 3,
              nrounds = 34,
              eta = 0.1)

property$pred_xg <- predict(xg, as.matrix(property[, 2:3]))

(property$price - property$pred_xg) ^ 2 %>% mean() %>% sqrt()
# [1] 104.8407

property$pred_xg <- NULL
set.seed(1)
folds <- kWayCrossValidation(nRows = nrow(property), nSplits = 3)

for(fold in folds) {
    xg <- xgboost(data = as.matrix(property[fold$train, 2:3]),
                  label = property[fold$train, 1],
                  nfold = 3,
                  nrounds = 40,
                  eta = 0.1)
    property[fold$app, "pred_xg"] <-
        predict(xg, as.matrix(property[fold$app, 2:3]))
}

(property$price - property$pred_xg) ^ 2 %>% mean() %>% sqrt()
# [1] 145.9076

Unfortunately, XGboost model does not achieve smaller RMSE than previous models.

As summary, tree based methods are not always better solution for prediction. As we see, the out-of-sample RMSE is similar to one for linear model. At the same time, tree-based methods lose precious interpretability.

Note: Both packages have built-in cross-validation functions. However, for proper comparison one has to train models on the same training data set applying, then, to the same test set.