A couple of weeks ago a colleague of mine asked me for a help to estimate Gerber-Shiu function by Monte-Carlo methods. The function is used in ruin theory for risk processes. One can think about this function as of equialence to a moment generating function. That is if the function is known, it is easy to derive a certain measurments of interest, for instance, a ruin probability. My colleague wants to estimate this function for an extenssion of Cramér–Lundberg model that includes positive jumps (capital injections). From the first glance it seems as a trivial task, but when I started approaching it, this problem turned out to be not so easy to solve.

Disclaimer: This post is outdated and was archived for back compatibility: please use with care! This post does not reflect the author’s current point of view and might deviate from the current best practices.

To estimate Gerber-Shiu function a large number of paths should be simulated. That’s why I firstly started with a function that simulates a path of the process. Basically, the random part of the model consists of two independent Poisson processes. There are three ways to simulate a Poisson process. The first method assumes simulating interarrival jumps’ times by Exponential distribution. The second method is to simulate the number of jumps in the given time period by Poisson distribution, and then the time of jumps by Uniform random variables. The third method requires a certain grid. Typically, only the former two methods are used.

During my first attamped I used the first method (i.e. simulating interarrival time by Exponential r.v.s). In order to check myself, I estimated ruin probabilities and compared with numerically derived in literature. For some reason, the estimated values of such simulated processes were not in line with numerical ones. I tried the second method, which yielded values closer to true ones. On the other hand, numerical values might be also bised due to the precision error. To find which values are correct I simplified the process to have only deterministic unit jumps, but still measurments were bised (this will be discussed in details in the next post). Further simplification led to a simple Poisson process, which is a focus of this post.

The mentioned above two methods of Poisson process simulation are widely covered in all simulation books. However, I have not found any information which method is better or at least any information about the speed of convergence. So I implemented my versions of algorithms (both algorithms can be found in references below). Note that my implementation is probably far away from the efficient one, but my goal is rather compare visually how fast these algorithms converge.

Method 1

This algorithm exploits the fact that interarrival times are exponentially distributed. We simulate the arrival times until the maximum time horizon is achieved.

sim_pp1 <- function(t, rate) {

    path <- matrix(0, nrow = 1, ncol = 2)

    jumps_time <- rexp(1, rate)

    while(jumps_time[length(jumps_time)] < t) {

        jump <- matrix(c(jumps_time[length(jumps_time)], path[nrow(path), 2],
                         jumps_time[length(jumps_time)], path[nrow(path), 2]  + 1),
                       nrow = 2, ncol = 2, byrow = TRUE)

        path <- rbind(path, jump)

        jumps_time <- c(jumps_time,
                        jumps_time[length(jumps_time)] + rexp(1, rate))
    }

    path <- rbind(path,
                  c(t, path[nrow(path), 2]))

    list(path, jumps_time)
}

Method 2

This method simulates the number of jumps by Possion random variable with the rate equals to the product of the time horizon and the process’s rate. Then, to calculate arrival times, random variables with uniform distribution are generated and ordered after (again, these algorithms are well-known and described in details in references).

sim_pp2 <- function(t, rate) {

    path <- matrix(0, nrow = 1, ncol = 2)

    jumps_number <- rpois(1, lambda = rate * t)
    jumps_time <- runif(n = jumps_number, min = 0, max = t) %>% sort()

    for(j in seq_along(jumps_time)) {
        jump <- matrix(c(jumps_time[j], path[nrow(path), 2],
                         jumps_time[j], path[nrow(path), 2]  + 1),
                       nrow = 2, ncol = 2, byrow = TRUE)
        path <- rbind(path, jump)
    }

    path <- rbind(path,
                  c(t, path[nrow(path), 2]))

    list(path, jumps_time)

}

Validation

Now, let’s check a couple of thigs, such as mean and vairance of interarrival times and their histogram for both methods.

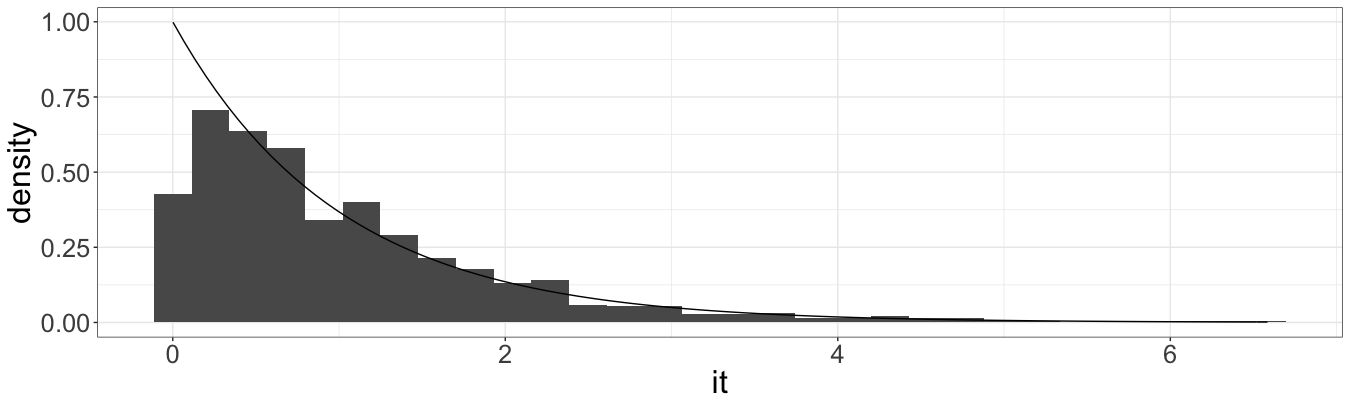
For the first method:

library("ggplot2")
library("magrittr")

set.seed(1)

path1 <- sim_pp1(1000, 1)
mean(diff(path1[[2]])); var(diff(path1[[2]]))
# [1] 1.029312
# [1] 0.9722406

data.frame(it = diff(path1[[2]])) %>%
    ggplot() +
    geom_histogram(aes(it, y = ..density..)) +
    stat_function(fun = dexp) +
    theme_bw() +
    theme(text = element_text(size = 24))

And for the second:

path2 <- sim_pp2(1000, 1)
mean(diff(path2[[2]])); var(diff(path2[[2]]))
# [1] 1.006302
# [1] 1.066079

data.frame(it = diff(path2[[2]])) %>%
    ggplot() +
    geom_histogram(aes(it, y = ..density..)) +
    stat_function(fun = dexp) +
    theme_bw() +
    theme(text = element_text(size = 24))

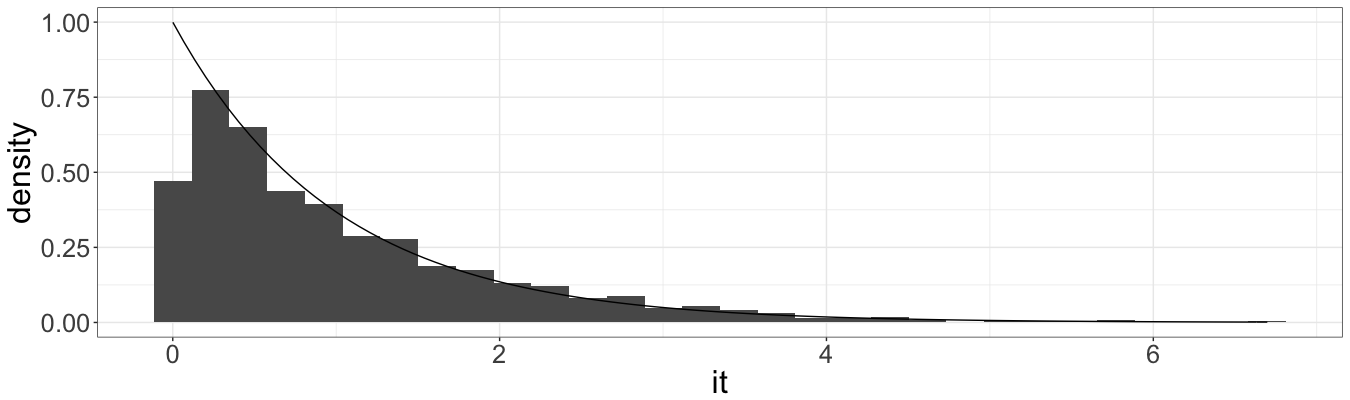
It seems that all values are in line with theory, that is the expected value and variance of interarrival times both equals to one (given the unit rate of Poisson process), as well as the shape of histograms.

Convergence

Mathmatically, both methods should have more or less the same speed of convergence. To check this we simulate 2000 paths with both methods and then estimate the expected value of the process at time ten as a function of the number of simulations.

t <- 10
n <- 2000
rate = 1

paths1 <- replicate(n = n, expr = sim_pp1(t, rate), simplify = FALSE)
means1 <- sapply(1:n,
                 function(x) {
                     pathes <- paths1[1:x]
                     mean(sapply(pathes, function(y) y[[1]][nrow(y[[1]]), 2]))
                 })

paths2 <- replicate(n = n, expr = sim_pp2(t, rate), simplify = FALSE)
means2 <- sapply(1:n,
                 function(x) {
                     pathes <- paths2[1:x]
                     mean(sapply(pathes, function(y) y[[1]][nrow(y[[1]]), 2]))
                 })

rbind(data.frame(n = 1:n, mean = means1, method = "1"),
    data.frame(n = 1:n, mean = means2, method = "2")) %>%
    ggplot() +
    geom_line(aes(x = n, y = mean, color = method)) +
    geom_hline(yintercept = rate * t) +
    theme_bw() +
    theme(text = element_text(size = 24))

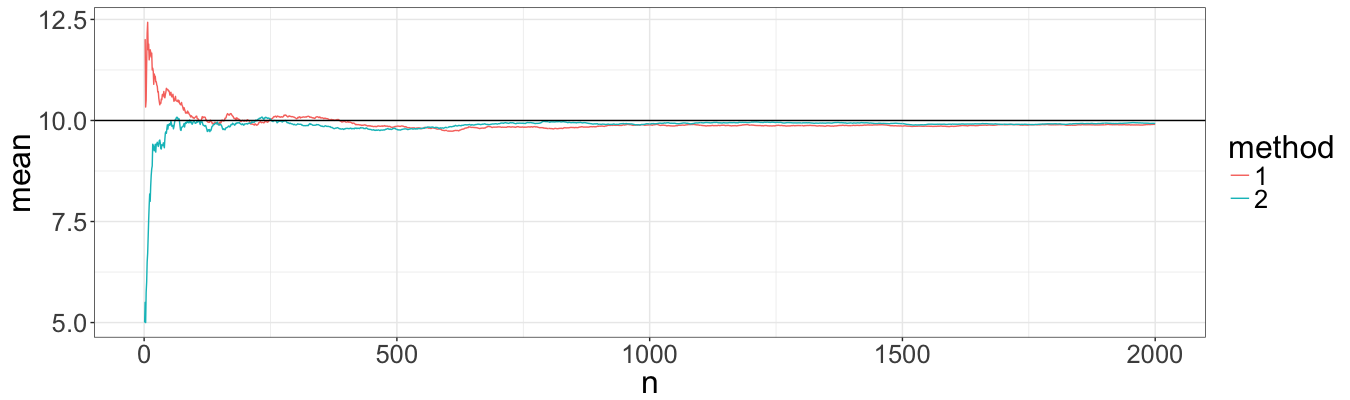
Indeed, visually the estimation of expected value convergence approximately with the same speed. However, I had problems with probabilities, and below I performed the same procedure but for the probability of a path to be below ten.

paths1 <- replicate(n = 2000, expr = sim_pp1(10, 1), simplify = FALSE)
probs1 <- sapply(1:2000,
                 function(x) {
                     pathes <- paths1[1:x]
                     mean(sapply(pathes, function(y) y[[1]][nrow(y[[1]]), 2]) <= 10)
                 })

paths2 <- replicate(n = 2000, expr = sim_pp2(10, 1), simplify = FALSE)
probs2 <- sapply(1:2000,
                 function(x) {
                     pathes <- paths2[1:x]
                     mean(sapply(pathes, function(y) y[[1]][nrow(y[[1]]), 2]) <= 10)
                 })

rbind(data.frame(n = 1:n, prob = probs1, method = "1"),
      data.frame(n = 1:n, prob = probs2, method = "2")) %>%
    ggplot() +
    geom_line(aes(x = n, y = prob, color = method)) +
    geom_hline(yintercept = ppois(q = 10, lambda = t * rate)) +
    theme_bw() +
    theme(text = element_text(size = 24))

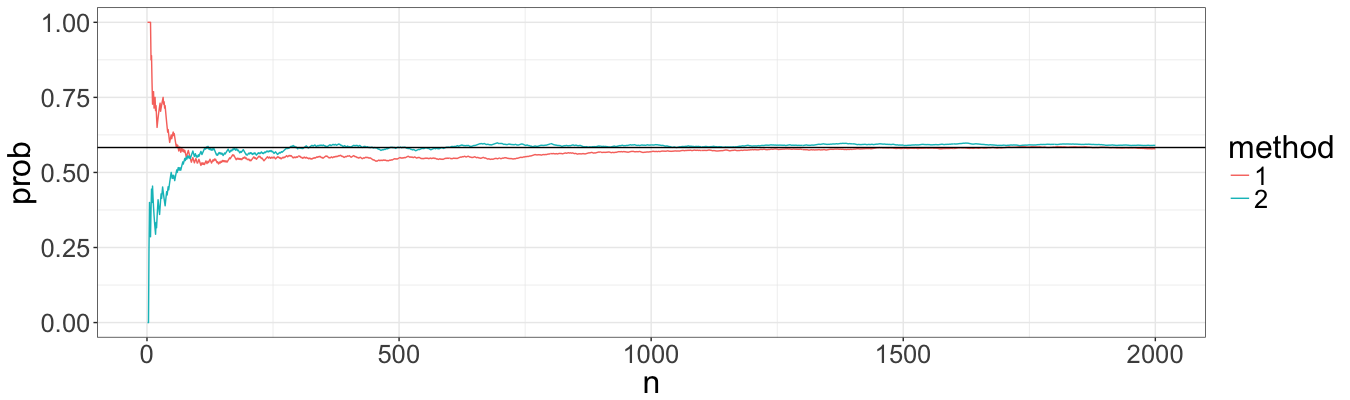
Again, methods seem to have the same performance. This is a good sign, because now I can compare methods for slightly more complicated models not being affraid that differences might be due to Poisson process simulation algorithms.